《线性代数》自学考试大纲
课程性质与目标
线性代数是高等院校理工科、经管类等专业的一门重要基础数学课程,本课程的主要任务是向学生介绍线性代数的基本概念、理论和方法,培养学生的抽象思维能力、逻辑推理能力、空间想象能力和利用线性代数知识分析和解决实际问题的能力。
通过本课程的学习,考生应达到以下目标:

- 掌握行列式、矩阵、向量、线性方程组、特征值与特征向量等核心概念。
- 理解并能够熟练运用相关定理和性质进行计算和证明。
- 具备运用线性代数知识解决实际问题的能力,特别是求解线性方程组。
- 为后续专业课程的学习和科研工作打下坚实的数学基础。
考试内容与考核要求
本大纲将考试内容分为七个主要模块,并对每个模块的知识点提出了“了解”、“理解”、“掌握”和“熟练掌握”四个不同层次的考核要求。
- 了解: 对所列知识内容有初步的认识,能够说出其大意,并在有关的问题中识别和再现。
- 理解: 对所列知识内容有较深刻的理性认识,能够解释其确切含义,并能分析和解决简单问题。
- 掌握: 在理解的基础上,能够运用所学知识解决较复杂的问题。
- 熟练掌握: 在掌握的基础上,能够灵活、综合地运用所学知识解决较复杂的问题。
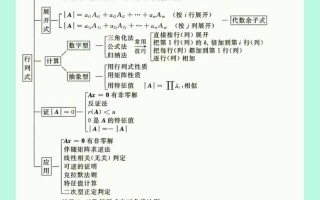
行列式
| 知识点 | 考核要求 | 说明 |
|---|---|---|
| 行列式的定义 | ||
| - 二阶与三阶行列式的定义 | 理解 | 熟悉对角线法则。 |
| - n阶行列式的定义(排列与逆序数) | 了解 | 理解逆序数的概念,了解n阶行列式的展开式。 |
| 行列式的性质 | ||
| - 行列式的基本性质(如转置、交换行/列、数乘、拆分等) | 掌握 | 重点掌握性质及其应用,能简化行列式计算。 |
| - 行列式的展开定理(按行/列展开) | 熟练掌握 | 这是计算行列式的核心方法,必须熟练掌握。 |
| 行列式的计算 | ||
| - 利用性质和展开定理计算具体行列式 | 熟练掌握 | 包括数字行列式、字母行列式。 |
| - 特殊行列式的计算(如上/下三角、对角、范德蒙德行列式等) | 掌握 | 记住常见特殊行列式的结果。 |
| - 克拉默法则 | 掌握 | 理解其理论意义,并能用于求解特殊的线性方程组。 |
矩阵
| 知识点 | 考核要求 | 说明 |
|---|---|---|
| 矩阵的概念 | ||
| - 矩阵的定义、表示法、同型矩阵、相等矩阵 | 理解 | 理解矩阵是一个数表,与行列式有本质区别。 |
| - 几种特殊矩阵(单位阵、对角阵、三角阵、对称阵、反对称阵等) | 掌握 | 能识别和写出这些特殊矩阵。 |
| 矩阵的运算 | ||
| - 矩阵的加法、数乘、乘法、转置运算及运算律 | 熟练掌握 | 矩阵乘法是重点和难点,必须理解其定义(行乘列)和运算规则(不满足交换律)。 |
| - 方阵的行列式、伴随矩阵 | 掌握 | 理解伴随矩阵的定义,掌握 A*A* = A*A = |A|E。 |
| 逆矩阵 | ||
| - 逆矩阵的定义与性质 | 理解 | 掌握逆矩阵的唯一性和相关性质。 |
| - 矩阵可逆的充分必要条件 | 掌握 | A 可逆 ⇔ |A| ≠ 0。 |
| - 逆矩阵的求法(伴随矩阵法、初等变换法) | 熟练掌握 | 必须熟练掌握初等变换法求逆,这是考试的重点。 |
| 矩阵的秩 | ||
| - 矩阵的秩的概念 | 理解 | 理解矩阵的秩是其行(或列)向量组的最大线性无关组的向量个数。 |
| - 利用初等变换求矩阵的秩 | 熟练掌握 | 将矩阵化为行阶梯形,非零行的行数即为秩。 |
| 矩阵的初等变换与初等矩阵 | ||
| - 初等变换与初等矩阵的概念 | 理解 | 理解初等矩阵左乘(行变换)和右乘(列变换)的意义。 |
| - 初等变换的应用(求逆、求秩、解方程组) | 熟练掌握 | 这是贯穿整个线性代数计算的核心工具。 |
向量与线性方程组
| 知识点 | 考核要求 | 说明 |
|---|---|---|
| n维向量 | ||
| - n维向量的概念、线性运算 | 理解 | 向量是矩阵的特殊形式,其运算与矩阵一致。 |
| - 向量组的线性组合与线性表示 | 掌握 | 理解 β = k₁α₁ + ... + kₘαₘ 的含义。 |
| 向量组的线性相关性 | ||
| - 线性相关与线性无关的定义 | 理解 | 这是线性代数的核心概念,必须深刻理解。 |
| - 线性相关性的判定定理 | 掌握 | 重点掌握“部分相关,整体必相关”;“整体无关,部分必无关”等。 |
| - 向量组的最大线性无关组与秩 | 掌握 | 理解向量组的秩等于其构成的矩阵的秩。 |
| 线性方程组 | ||
| - 克拉默法则 | 掌握 | 见模块一。 |
| - 非齐次/齐次线性方程组有解的判定定理 | 熟练掌握 | r(A) = r(A|b) = n 有唯一解;r(A) = r(A|b) < n 有无穷多解;r(A) ≠ r(A|b) 无解。 |
| - 齐次线性方程组有非零解的判定定理 | 熟练掌握 | r(A) < n 有非零解。 |
| - 线性方程组解的结构 | 熟练掌握 | 这是本模块乃至全书的重中之重。 |
| - 齐次方程组的基础解系、通解 | 理解基础解系的定义,掌握求基础解系和通解的方法。 | |
| - 非齐次方程组的解的结构、通解 | 理解其通解 = 对应齐次方程的通解 + 非齐次方程的一个特解。 | |
| - 用初等变换法求解线性方程组 | 熟练掌握 | 考试中最常见的计算题型。 |
向量空间
| 知识点 | 考核要求 | 说明 |
|---|---|---|
| 向量空间的基本概念 | ||
| - 向量空间的定义、子空间 | 了解 | 理解公理化定义,能判断一个集合是否为子空间。 |
| - 基、维数、坐标 | 理解 | 理解基是线性无关的生成集,维数是基中向量的个数。 |
| - 基变换与坐标变换 | 掌握 | 掌握过渡矩阵的概念,能进行基变换和坐标变换的计算。 |
| 向量的内积 | ||
| - 内积的定义、性质 | 理解 | 掌握标准内积(点积)的计算。 |
| - 向量的长度(范数)、夹角、正交 | 掌握 | 掌握向量的模、夹角公式,理解正交的概念。 |
| - 施密特正交化过程 | 掌握 | 能将一组线性无关的向量组正交化和单位化。 |
| - 正交矩阵的定义与性质 | 掌握 | 理解 Q⁻¹ = Qᵀ,其行/列向量组是标准正交的。 |
特征值与特征向量
| 知识点 | 考核要求 | 说明 |
|---|---|---|
| 特征值与特征向量的定义与性质 | ||
| - 特征值与特征向量的定义 | 理解 | 理解 Ax = λx 的几何意义。 |
| - 特征值与特征向量的求法 | 熟练掌握 | 解特征方程 |A - λE| = 0 求特征值,再解 (A - λE)x = 0 求特征向量。 |
| - 特征值与特征向量的性质 | 掌握 | 如特征值之和等于迹,特征值之积等于行列式等。 |
| 相似矩阵 | ||
| - 相似矩阵的定义与性质 | 理解 | 理解 B = P⁻¹AP 的含义。 |
| - 矩阵可对角化的条件 | 掌握 | n 阶方阵 A 可对角化 ⇔ A 有 n 个线性无关的特征向量。 |
| - 矩阵的对角化 | 熟练掌握 | 掌握求可逆矩阵 P 和对角阵 的方法。 |
二次型
| 知识点 | 考核要求 | 说明 |
|---|---|---|
| 二次型及其矩阵表示 | ||
| - 二次型的定义、矩阵表示 | 理解 | 任何一个二次型都可以唯一地对应一个对称矩阵。 |
| - 合同变换与合同矩阵 | 了解 | 理解 CᵀAC 的含义。 |
| 化二次型为标准形和规范形 | ||
| - 用配方法化二次型为标准形 | 掌握 | 必须掌握此方法。 |
| - 用正交变换化二次型为标准形 | 熟练掌握 | 这是本模块的重点,本质上是矩阵对角化的应用。 |
| - 二次型的规范形 | 了解 | 理解惯性定理。 |
| 正定二次型与正定矩阵 | ||
| - 正定二次型与正定矩阵的定义 | 理解 | 理解 xᵀAx > 0 对所有非零 x 成立。 |
| - 正定矩阵的判定法 | 掌握 | 掌握主要判定方法:1. 特征值全为正;2. 顺序主子式全为正。 |
考试方式与试卷结构
- 考试方式: 闭卷,笔试。
- 考试时间: 150分钟。
- 满分: 100分。
- 试卷结构(参考):
- 选择题/填空题 (约30-40分): 考查基本概念、性质和简单计算。
- 计算题 (约40-50分): 考查行列式、矩阵运算、求解方程组、求特征值与特征向量、二次型化标准形等核心计算能力,这是分值最高的部分。
- 证明题/综合应用题 (约20-30分): 考查对定理的理解、逻辑推理能力和综合运用知识解决复杂问题的能力,证明向量组的相关性、矩阵可对角化的条件、二次型正定性的判定等。
自学建议
- 教材选择: 选择一本经典的线性代数教材,如同济大学《线性代数》(国内高校通用),或 Gilbert Strang 的《Introduction to Linear Algebra》(英文原版或译本,侧重直观理解)。
- 注重概念,而非死记: 线性代数的概念环环相扣,务必理解“线性相关”、“秩”、“特征值”等核心概念的内涵和外延,而不仅仅是记住定义。
- 动手计算,勤加练习: 线性代数是一门工具性学科,不做题是学不会的,从基本运算到综合应用题,都要亲自动手做,特别是求解线性方程组和矩阵对角化这类大题。
- 构建知识网络: 画思维导图,将行列式、矩阵、向量、方程组、特征值、二次型等模块串联起来,矩阵的秩如何联系到方程组的解?特征值如何用于矩阵对角化?对角化又如何用于二次型化标准形?
- 重视证明过程: 证明题能检验你对知识的深刻理解,尝试自己推导一些重要定理,如“秩等于行秩等于列秩”。
- 利用资源: 可以在网上寻找优质的教学视频(如B站、MIT OpenCourseWare)、在线计算工具(如WolframAlpha)来辅助学习和验证计算结果。
祝你自学顺利,考试成功!

版权声明:除非特别标注,否则均为本站原创文章,转载时请以链接形式注明文章出处。