牛头刨床课程设计如何优化传动与运动精度？

99ANYc3cd6 课程介绍 2025-12-02 1

机械原理课程设计：牛头刨床设计指南

设计任务与要求

设计题目： 牛头刨床主体机构（通常为导杆机构）的运动分析、动态静力分析及飞轮转动惯量计算。

已知条件（通常由指导老师给定，以下为常见示例）：

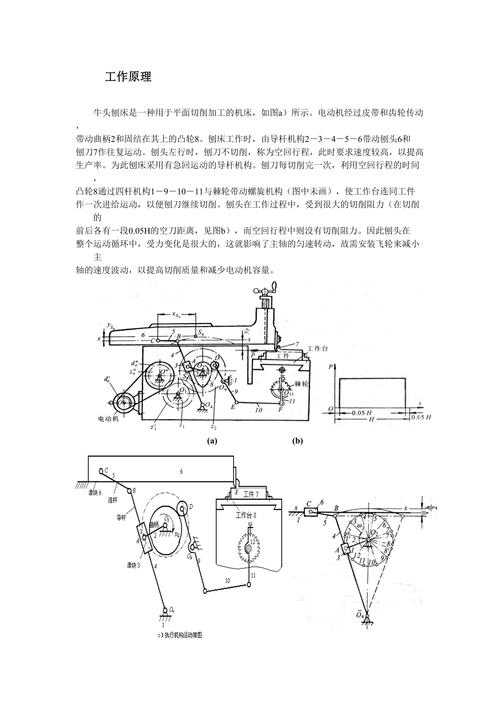
刨刀行程 (H): 250 mm
行程速比系数 (K): 1.5
刨刀切削阻力 (P_Q): 5000 N (这是一个恒定值，简化处理)
工作阻力变化规律： 通常简化为在一个工作循环内，只在切削行程有恒定阻力，空行程阻力忽略不计。
曲柄转速 (n_1): 60 r/min (即 ω₁ = 2πn₁/60 ≈ 6.28 rad/s)
机构各杆长度比例： 设曲柄长度 l_AB = 100 mm，作为其他尺寸的设计基准。

设计要求：

方案设计： 选择合适的机构方案，绘制机构运动简图。
运动分析： 对机构进行位移、速度、加速度分析，并绘制相应的线图。
动态静力分析： 计算各运动副中的反力，并绘制平衡力矩（或平衡力）随曲柄转角变化的线图。
飞轮设计： 计算在一个运动周期内盈亏功的最大值，确定安装飞轮所需的转动惯量。
撰写设计说明书： 详细阐述设计过程、计算结果和分析结论。
绘制图纸： 绘制机构运动简图、速度多边形、加速度多边形及力分析图等。

设计步骤详解

第一步：方案设计与机构运动简图绘制

机构选择： 牛头刨床的主体运动机构通常采用摆动导杆机构，因为该机构具有急回特性，能很好地满足刨床“慢速切削、快速退回”的工艺要求，行程速比系数 K > 1。
- 优点： 结构简单、传力性能好、具有急回特性。
- 构成： 由机架、曲柄（输入件）、滑块和导杆（执行件）组成。
确定机构尺寸参数： 这是设计的核心第一步，直接关系到后续所有分析。
- 计算极位夹角 (θ): θ = 180° * (K - 1) / (K + 1) 示例：K=1.5，则 θ = 180° (1.5-1)/(1.5+1) = 36°*
- 确定曲柄长度 (l_AB): H = 2 * l_AB * sin(θ/2) 由此可反推出曲柄长度： l_AB = H / (2 * sin(θ/2)) 示例：H=250mm, θ=36°，则 l_AB = 250 / (2 sin(18°)) ≈ 405.4 mm，为简化计算，可取 l_AB = 400 mm 或 410 mm，然后重新计算 H 或 K，使其满足原始要求。*
- 确定机架长度 (l_AC): 在摆动导杆机构中，机架长度 l_AC 是导杆摆动中心 A 到曲柄回转中心 C 的距离，为保证曲柄能整周转动，必须满足 l_AC > l_AB，通常取 l_AC = l_AB / cos(θ/2) 或 l_AC = 1.2 ~ 1.5 * l_AB。 示例：取 l_AC = 1.4 l_AB = 1.4 400 = 560 mm。
- 确定导杆长度 (l_BD): 导杆长度 l_BD 决定了刨刀的切削位置，通常根据机床的总体布局和结构要求来确定，只要保证刨刀能完成行程即可，可取 l_BD = 1.5 * H = 375 mm。
绘制机构运动简图： 根据计算出的 l_AB, l_AC, l_BD，按比例绘制出牛头刨床的机构运动简图，并标注出各构件和运动副的编号（如曲柄1，导杆3，滑块2，机架4等）。

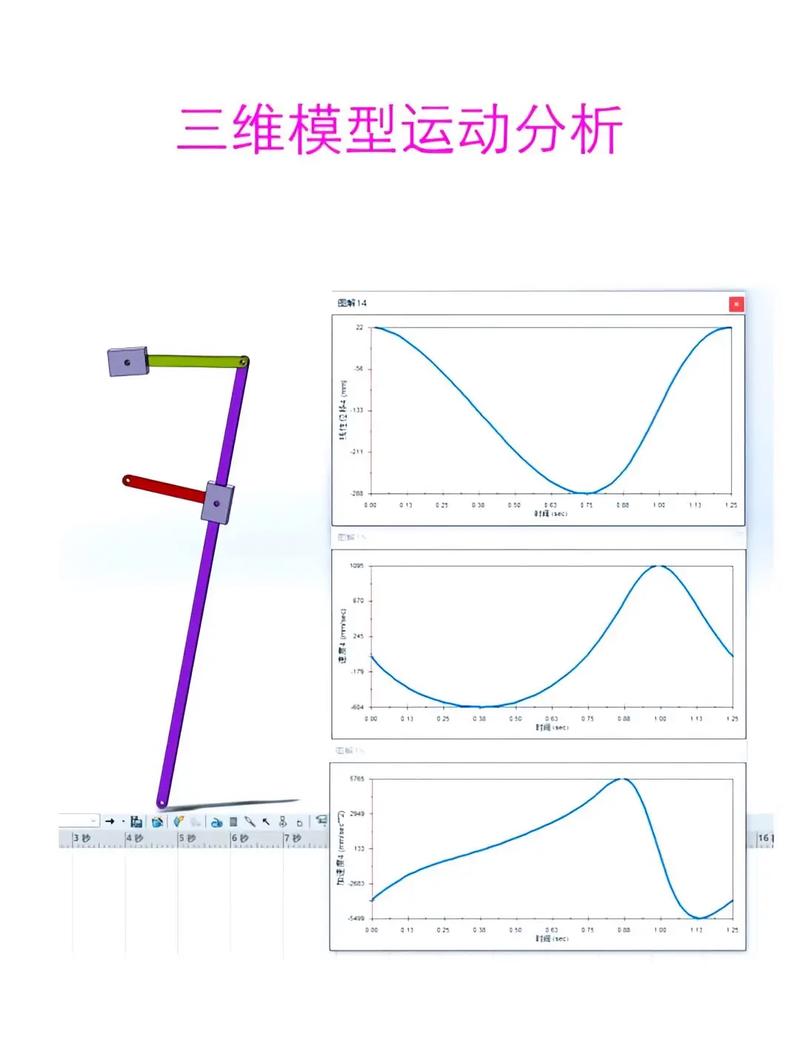
第二步：运动分析

运动分析是力分析和动力学分析的基础,通常采用图解法（课程设计常用）或解析法（编程计算，精度高）。

建立坐标系： 以机架回转中心 C 为原点建立直角坐标系。
位移分析：
- 导杆3的角位移 (φ₃): φ₃ = arctan(l_AB * sinφ₁ / (l_AC + l_AB * cosφ₁)) φ₁ 是曲柄1的转角，从 0° 到 360° 变化。
- 刨刀（滑块D）的位移 (s_D): s_D = l_BD * (1 - cosφ₃) (以导杆右极限位置为位移零点)
速度分析：
- 使用矢量方程图解法（速度多边形）。
- 矢量方程： v_B3 = v_B2 + v_B3B2
  - v_B3: 导杆3上B点的绝对速度，方向垂直于AB。
  - v_B2: 曲柄1上B点的绝对速度，v_B2 = ω₁ * l_AB，方向垂直于AB。
  - v_B3B2: 滑块2相对于导杆3的相对速度，方向沿导杆BD。
- 步骤：
  1. 选定速度比例尺 μ_v (单位: m/s/mm)。
  2. 从极点 p 出发，作 pb 代表 v_B2。
  3. 过 b 点作 v_B3B2 的方向线（平行于BD）。
  4. 过 p 点作 v_B3 的方向线（垂直于AB）。
  5. 两方向线交于 b3 点，则 pb3 代表 v_B3，bb3 代表 v_B3B2。
- 刨刀速度 (v_D): v_D = v_B3 * (l_BD / l_AB) (因为导杆3作定轴转动，其上各点速度与到A点的距离成正比)
加速度分析：
- 使用矢量方程图解法（加速度多边形）。
- 矢量方程： a_B3 = a_B2 + a_B3B2^k + a_B3B2^r
  - a_B3: 导杆3上B点的绝对切向加速度，方向垂直于AB。
  - a_B2: 曲柄1上B点的绝对向心加速度，a_B2 = ω₁² * l_AB，方向沿BA。
  - a_B3B2^k: 哥氏加速度，a_B3B2^k = 2 * ω₃ * v_B3B2，方向将 v_B3B2 沿 (即 a_B3 的方向) 旋转90°。
  - a_B3B2^r: 滑块2相对于导杆3的相对加速度，方向沿BD。
- 步骤：
  1. 选定加速度比例尺 μ_a (单位: m/s²/mm)。
  2. 从极点 p' 出发，作 p'b' 代表 a_B2。
  3. 过 b' 点作 a_B3B2^k 的矢量。
  4. 过 a_B3B2^k 的矢端作 a_B3B2^r 的方向线（平行于BD）。
  5. 过 p' 点作 a_B3 的方向线（垂直于AB）。
  6. 两方向线交于 b3' 点，则 p'b3' 代表 a_B3，b'k 代表 a_B3B2^k，kb3' 代表 a_B3B2^r。
- 刨刀加速度 (a_D): a_D = a_B3 * (l_BD / l_AB)
绘制线图： 将计算或图解得到的 s_D, v_D, a_D 随曲柄转角 φ₁ 的变化数据，整理成表格，并绘制成 s_D-φ₁, v_D-φ₁, a_D-φ₁ 曲线图。

第三步：动态静力分析

目的是求出为了维持系统匀速运转,需要加在曲柄上的平衡力矩 M_b，以及各运动副的反力。

确定构件质量与转动惯量（简化处理）：
- 刨刀（滑块D）： 假设其质量为 m_D，则惯性力 F_ID = -m_D * a_D，方向与 a_D 相反。
- 导杆3： 假设其质心在 S₃ 点，质量为 m_3，转动惯量为 J_S3，则惯性力 F_I3 = -m_3 * a_S3，惯性力矩 M_I3 = -J_S3 * α₃ (α₃为导杆角加速度)。
- 曲柄1： 通常认为其质心在 C 点，质量 m_1，转动惯量 J_C，惯性力为零，惯性力矩 M_I1 = -J_C * α₁，由于 ω₁ 恒定，α₁=0，故 M_I1 = 0。
- 滑块2： 质量较小，通常忽略其惯性力。
列静力平衡方程并图解： 从执行件（刨刀）开始，依次拆分构件，进行力分析。
- 分析刨刀（滑块D）：
  - 受力：切削阻力 P_Q (向左)，导杆对它的反力 R_43 (沿导杆方向)，惯性力 F_ID (向右)。
  - 平衡方程：ΣF = 0，这三个力构成封闭的力三角形。
  - 图解： 选定力比例尺 μ_F，作已知力 P_Q 和 F_ID 的矢量，首尾相连，然后连接起点和终点，得到 R_43 的矢量，可求出 R_43 的大小和方向。
- 分析导杆3：
  - 受力：刨刀对它的反力 R_34 (与 R_43 大小相等，方向相反)，机架对它的反力 R_14 (通过A点)，曲柄对它的反力 R_23 (通过B点)。
  - 平衡方程：ΣF = 0 和 ΣM_A = 0。
  - 图解： R_34 已知。R_14 和 R_23 的方向线已知（均通过A点），三个力汇交于一点，构成封闭的力三角形，可求出 R_14 和 R_23。
- 分析曲柄1：
  - 受力：机架对它的反力 R_41 (与 R_14 大小相等，方向相反)，连杆对它的反力 R_32 (与 R_23 大小相等，方向相反)，平衡力矩 M_b (驱动力矩)。
  - 平衡方程：ΣM_C = 0。
  - 计算： M_b = R_32 * l_h，l_h 是 R_32 对 C 点的力臂，力臂 l_h 可以通过几何关系从图中量取。
绘制线图： 将计算得到的平衡力矩 M_b 随曲柄转角 φ₁ 的变化数据，绘制成 M_b-φ₁ 曲线图。

第四步：飞轮转动惯量计算

飞轮的作用是储存和释放能量,以克服周期性变化的盈亏功，使主轴（曲柄）的转速波动在允许范围内。

计算驱动力矩 (M_d)： 假设驱动力矩 M_d 为常数，则在一个周期内，驱动力所做的功等于阻力所做的功。 W_d = W_r M_d * 2π = ∫[0 to 2π] M_b(φ₁) dφ₁ M_d = (1 / 2π) * ∫[0 to 2π] M_b(φ₁) dφ₁ 积分 ∫M_b(φ₁)dφ₁ 可以用近似积分法（如梯形法或辛普森法）根据 M_b-φ₁ 曲线图的数据进行计算。
计算盈亏功 (ΔW)： 在任意转角 φ 处，盈亏功 ΔW(φ) 是驱动力矩做功与阻力矩做功的差值。 ΔW(φ) = ∫[0 to φ] (M_d - M_b(φ₁)) dφ₁ 根据计算结果，找出 ΔW(φ) 的最大值 ΔW_max 和最小值 ΔW_min。
计算最大盈亏功 (W_y)： W_y = ΔW_max - ΔW_min
计算飞轮转动惯量 (J_F)： J_F = W_y / (δ * ω_m²)
- 速度不均匀系数，根据课程设计要求给定（如 δ = 1/20 ~ 1/30）。
- ω_m: 平均角速度，ω_m = (ω_max + ω_min) / 2 ≈ ω₁ (因为波动不大)。

设计说明书与图纸

设计说明书：
- 封面（题目、姓名、学号、日期）
- 目录
- 设计任务书
- 方案设计与论证（说明为何选择摆动导杆机构）
- 机构运动学分析（详细列出公式、计算过程、表格数据）
- 动态静力分析（详细列出公式、计算过程、表格数据）
- 飞轮设计（详细列出公式、计算过程）
- 设计总结与心得体会
- 参考文献
图纸：
- A2或A1图纸一张，包含以下内容：
  - 机构运动简图 (按比例绘制，标注尺寸)
  - 速度多边形 (至少一个位置)
  - 加速度多边形 (至少一个位置)
  - 力分析图 (至少一个位置)
  - 主要线图 (s_D-φ₁, v_D-φ₁, a_D-φ₁, M_b-φ₁)
- 所有图都应有清晰的标题、比例尺、必要的说明和标注。