数学与应用数学师范类课程如何培养未来教师？

99ANYc3cd6 课程介绍 2025-11-30 1

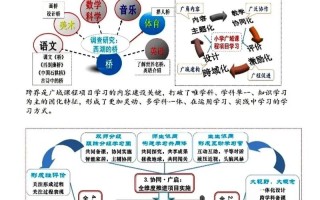
通识教育课程、学科基础课程、专业核心课程、教师教育与实践课程，下面我将为您详细解析每个模块下的具体课程。

通识教育课程

这类课程是所有大学生的必修课,旨在提升学生的综合素质、人文素养和科学精神。

思想政治理论类： 《马克思主义基本原理》、《毛泽东思想和中国特色社会主义理论体系概论》、《中国近现代史纲要》、《思想道德修养与法律基础》、《形势与政策》等。
大学外语： 通常为大学英语，培养学生的英语听、说、读、写能力。
计算机基础： 《大学计算机基础》、《Python程序设计基础》等，培养学生的信息素养和计算思维。
大学体育： 培养学生的健康体魄和运动习惯。
人文社科与艺术类： 如《大学语文》、《逻辑学》、《心理学导论》、《音乐欣赏》、《美术鉴赏》等，拓宽知识面，提升审美和人文情怀。

学科基础课程

这是数学专业的基石,旨在为学生构建一个严谨、系统的现代数学知识框架，这些课程通常在大学一、二年级完成，难度较大，是区分数学专业与其他专业的关键。

数学分析: 数学专业最重要、最核心的基础课，内容涵盖极限、导数、积分、级数等，是整个高等数学的理论深化，对逻辑思维和抽象能力的培养至关重要。
高等代数: 线性代数的理论深化版，主要研究多项式、行列式、矩阵、线性方程组、线性空间、线性变换等，是现代数学的通用语言。
解析几何: 用代数方法研究几何问题，为后续的数学分析、高等代数提供直观的几何背景，并引入向量空间等概念。
常微分方程: 研究含有未知函数及其导数的方程，是描述自然界中变化规律的重要工具，在物理、工程、经济等领域有广泛应用。

专业核心课程

在学科基础之上,这些课程进一步深化和拓展学生的数学专业知识，并开始与应用领域结合。

复变函数: 将实数域的微积分推广到复数域，在信号处理、流体力学等领域有重要应用。
概率论与数理统计: 研究随机现象的数量规律，是现代数据科学和人工智能的理论基础。
实变函数与泛函分析: 将微积分的理论建立在更严谨的集合论和测度论基础上，是现代分析学的前沿课程。
抽象代数: 研究各种代数结构（如群、环、域），是纯粹数学的核心分支之一，极大地锻炼抽象思维能力。
数值分析/计算方法: 研究如何使用计算机算法解决数学问题，是连接理论与应用、数学与计算机的桥梁。
数学建模: 综合运用数学知识、计算机技术和分析技巧，解决实际问题的课程，是培养应用能力的核心环节。
微分几何: 用微积分的方法研究曲线和曲面，是爱因斯坦广义相对论的数学语言。
拓扑学: 研究空间在连续变形下保持不变的性质，被称为“橡皮几何学”，是高度抽象的数学分支。
离散数学: 包含数理逻辑、集合论、图论等内容，是计算机科学的数学基础。

教师教育与实践课程

这是师范类专业最核心、最特色的模块，旨在培养学生的教育教学技能和师德素养，将“数学家”培养成“教育家”。

教育学原理: 教育学的基础理论，探讨教育的本质、目的、制度和规律。
教育心理学: 研究学生在学习过程中的心理活动规律，为教学设计提供理论依据。
课程与教学论: 专门研究数学课程的设计、实施和评价的理论。
中学数学教材分析与教学设计: 师范类核心课程，深入研究中学数学课程标准，分析不同版本教材的编写思路，并学习如何进行一节课的教学设计。
中学数学教学技能: 师范类核心课程，系统训练导入、提问、讲解、板书、多媒体使用、课堂管理等教学基本功。
数学教育测量与评价: 学习如何科学地设计试卷、评价学生的学习效果，并进行教学反思。
数学思想方法与解题研究: 深入剖析中学数学知识背后蕴含的数学思想（如函数与方程思想、数形结合思想），并提升自身的解题能力和指导学生解题的能力。
师德修养与教师专业发展: 培养教师的职业道德，并规划未来的职业成长路径。
教育实践环节: 这是将理论付诸实践的关键环节，贯穿整个大学后期。
- 见习: 早期进入中学课堂，观察有经验教师的授课。
- 微格教学: 在模拟教室中进行片段教学，并由老师和同学进行点评。
- 实习: 到指定的中学进行为期数周或数月的全职教学实践，独立承担备课、上课、批改作业、组织班会等任务。
- 毕业论文/设计: 通常要求结合教育实践，完成一篇关于中学数学教学研究的论文。